Month: August 2016

Week 1: Creating a Culture of Math Discussions and Debates

Julia FinneyfrockLeave a comment

Starting my second year of teaching.Thankfully, I had one prep that didn’t change, Geometry! I’m finally out of the “holding my head up right above the water so I don’t drown” year and am finally truly changing and analyzing my classes. This year I decided to have two main goals.

  1. I want my students to speak and debate mathematically
  2. I want my students to write mathematically

For this post, I’m going to focus on goal #1.  In my first week back, I created more mathematical discussion than I had the entire previous year.

At Twitter Math Camp this summer, I went to a morning session with Mattie Baker and Chris Luzniak  about creating a culture of mathematical discussion and debate. One of the many ways to do this was to set up a classroom environment is which students use the format

My claim is____________. My warrant is _____________  to express and justify their ideas.

I started using this format on the first day of class. I started asking fun questions like “what’s your favorite movie?” “where’s your favorite vacation spot” and some “would you rather” questions. This was a great way to help students become comfortable with the format, get comfortable with each other, and helped me learn their names very quickly. We continued with these same type of questions on day two.

Next, I started asking more mathematical questions, specifically for vocab that they were supposed to look up the night before for homework. I called on two or three students per vocab word to hear their opinions. If there was a controversial word, I asked more students for their thoughts.   This was a great way to go over and discuss vocab in an interactive way. I could also see what misconceptions they had of certain words.

 

Then I used this to explore a topic that we hadn’t really focused on yet. For homework, I had students look up the definition of congruent and equal and compare them. When they submitted their responses I could tell that there were misconceptions. Students also didn’t know when to use equal versus congruent.  I decided to start the class with some claims and warrants. The entire class became involved in the discussion on where = or congruent belongs and WHY it belongs there.

I have also used this to discuss a topic that we learned the day before. Chris had a great activity debating if the best method of finding distance  is the Pythagorean theorem or the distance formula (depending on the information given). I let students work through the three distance problems but also provide a claim and warrant for why they chose that method. At the end of class, we shared our claim and warrants as a class.

I’ve really enjoyed implementing claim and warrants into my class so far. I can’t wait to try (and blog) once I try other things from this session!

Simplifying Rational Expressions: Mafia Edition

Julia FinneyfrockLeave a comment

When simplifying rational expressions, students always seem to want to simplify TOO much (and incorrectly) !! Below are a few common”over simplifications” that I’ve seen.

 

This is where #lifelessonswithFinney kicked in. We started talking about the Mafia. Yes, the Mafia. Not only were we talking about the Mafia, but we were talkinIMG_8864g about killing off family members of the Mafia.

The polynomial is our numerator is a family. The Mafia Family. The denominator is our hitman.

I asked my students what they thought would happen if they tried to kill only one member but not the rest of the family.

“We’d be in trouble!!!! They’d come after us!!!!!!!!!”

Exactly. So we if we want to kill off one member of the family then we have to kill them all! This is the only way that you’d make it out alive! If you can’t kill them all then it is fully simplified. Killing doesn’t mean you have to get rid of it completely. However, you must “hit” every member of the family. 

 

Making Percents Real : Apple Edu

Julia FinneyfrockLeave a comment

I just finished my first week of teaching Algebra 2 ever. On one of the first days, I wanted to dive in and do math, but I didn’t want to intimidate my students so early in the year. Julie Reulbach gave me the great idea of reviewing percents by looking at Apple Computers. Screen Shot 2016-08-22 at 4.56.01 PM

I handed out the sheet I created with no other instructions or introduction than they could work with a partner to figure out the answers.

The worksheet I created explored the 13-inch MacBook Pro. First, I had students find the tax  on the computer and then justify how they found it.

Next, we looked at the price of the 13-inch MacBook Pro compared to the price of the same computer from the Apple Education Store. Students had to find the percent discount.

IMG_8826
The students decided to name my lesson for me 

Third, students had to apply that percent discount to the cost of the 15 inch Macbook Pro to figure out what education price would be.

This is where the conversation became interesting. After everyone was finished, I revealed the actual education price of the Macbook. They were outraged!!! The price was about $100 more than they calculated it should be!!!

This then prompted the question “Do you think this happens for every Apple Product?”

Each group then picked an Apple product. We looked at Macbook Air, Ipads,  and Imacs (I have a class of 8 students).

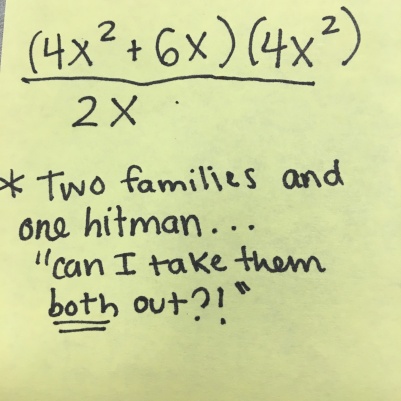
Students picked what size they first wanted to look at and then found the percent discount from the original price to the education price. Once they found the percent decrease they wrote their percent on the board. They then looked up a different size of the same producIMG_8825t to see if they discount remained the same!

This lead into a discussion about which product receives the biggest discount and why. Also what we thought affected the discount, and how sales aren’t always as straightforward as they seem.

This was a fun, easy, and real-world lesson that helped students review percents without sitting through a review lesson or by doing practice problems.

We did go over the worksheet to address any class misconceptions before we broke out to look up different products.  Originally, many students found the percent tax by finding the tax and then adding it to the original. This was a great opportunity to introduce original(1+percent) which they see for growth and decay later in the chapter.